ogtore.blogg.se - Factor quadratic equation

Tryįactorise each expression wherever possible. Now you are fully armed to tackle any quadratic expression. To make the factorisation correct we have to multiply by theĬoefficient of x 2 in the original quadratic, that is multiply by A.

The third and final complication occurs for quadratic expressions
Yes, we can express it as the product of two polynomial factors.
Since the product of those two factors is zero, then according to the Zero Product Rule, one of the factors must be equal to zero.
So we set each of the factors to zero and solve to determine the two possible solutions.
y2 6y + 5 0
(y 5) (y.

Type two identical factors for perfect squares, ( x+b)( x+b), or use the Excel and MATLAB Still more exercises for practice: Exerciseįactorise each expression wherever possible or type "Impossible". The next complication is that sometimes there If it cannot be factorised using real numbers. Root, so this quadratic cannot be factorised using real numbers.įactorise each expression wherever possible or type "Impossible" Indicates the quadratic cannot be factorised using real numbers. On the values of the coefficients) involves the square root of a negative number. When using this method to factorise a quadratic.įirstly, the formula sometimes (depending There are some complications that crop up The correct values will be substituted below. Here then is the strategy to use: ExampleĮnter the values of A, B and C for the expression

Knowing the solutions, we can then write down the factors as explained earlier. To the formula the solutions of the equation x 2 − 2 x − 15 = 0 are: The quadratic x 2 − 2 x − 15 has A = 1, B = −2 and C = −15. It says that The solutions of the equation A x 2 There is a formula for solving quadratic equations which you have probably seen before:

In this example, the two solutions are 5 and −3, and so the two factorsĪre ( x − 5) and ( x − ( −3)) which simplifies to ( x − 5) and ( x + 3).Īs though if we could solve quadratic equations, we could factorise quadratics. Looking at it the other way around, if we knew the solutions of theĮquation, we could find the factors: they just take the form ( x − (solution)). Therefore the two possible solutions of the equation are x = 5 and x = −3. So for the equation to hold, either x − 5 must be zero But a product of two factors can only be equal to zero if one or the If we factorise the quadratic, the equation can be written as ( x −ĥ)( x + 3) = 0.

In the solutions of the equation x 2 − 2 x − 15 = 0 (called a quadraticĮquation). Linear factors ( x − 5)( x + 3) which generate it when multiplied out. Muliplied out two linear factors to obtain a quadraticĮxpression by using the distributive law.Ī quadratic we have to go from an expression such as x 2 − 2 x − 15 to the Is the reverse of multiplications such as this:

Tangents, Derivatives and Differentiationįactorisation is the reverse of multiplying out.

Rearranging Equations III (Harder Examples).

Rearranging Equations II (Quadratic Equations).

Rearranging Equations I (Simple Equations).

Order of Operations for Algebraic Expressions.

Step 4: Equate each factor to zero and figure out the roots upon simplification. Step 3: Use these factors and rewrite the equation in the factored form. Step 2: Determine the two factors of this product that add up to 'b'. Once you are here, follow these steps to a tee and you will progress your way to the roots with ease. You can also use algebraic identities at this stage if the equation permits. Either the given equations are already in this form, or you need to rearrange them to arrive at this form. Keep to the standard form of a quadratic equation: ax 2 + bx + c = 0, where x is the unknown, and a ≠ 0, b, and c are numerical coefficients. The quadratic equations in these exercise pdfs have real as well as complex roots. Backed by three distinct levels of practice, high school students master every important aspect of factoring quadratics.

Convert between Fractions, Decimals, and PercentsĬatapult to new heights your ability to solve a quadratic equation by factoring, with this assortment of printable worksheets.

Converting between Fractions and Decimals.

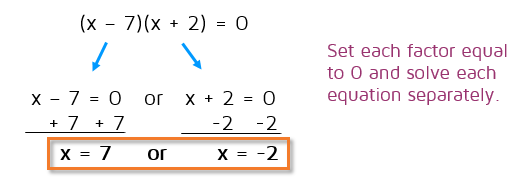
Parallel, Perpendicular and Intersecting Lines.